近日，南方科技大学力学与航空航天工程系教授邓巍巍团队关于液滴动态旋涂方面的研究取得新进展，成果以“On axisymmetric dynamic spin coating with a single drop of ethanol”为题在流体力学权威期刊Journal of Fluid Mechanics上发表。该研究发现动态旋涂可分为惯性驱动和离心驱动的两个阶段，并揭示了各自阶段液滴铺展规律。

旋涂是利用离心力将基底上的液体展开形成薄膜的工艺。旋涂装置简洁，可较容易获得厚度均匀性优于1%的亚微米薄膜。由于旋涂工艺制膜具有很好的均匀性、重复性以及制备的器件性能较高等特点，被广泛用于光刻胶镀膜、有机光伏电池、钙钛矿光伏电池等领域。在旋涂过程中，基底可以处于旋转状态再滴加液体(称为“动态旋涂”或dynamic spin-coating)，或者涂覆液体覆盖基底后开始旋转(称为“静态旋涂”，或static spin-coating)。其中，动态旋转有一些明显的优势：因为它需要的覆膜材料较少，材料利用率高。例如，在典型的一厘米见方的基片上，静态旋涂需要几十微升溶液，而动态旋涂只需要约6微升。对于逐层涂覆多层覆膜，如果溶剂不是严格正交的，动态旋涂可减少对前一层的二次溶解。此外，动态旋涂包含液滴撞击旋转基底的过程，其惯性冲击可以完成初始铺展，可在较低转速使用。在流体力学中，旋涂过程也是一个经典的研究对象。然而，之前多数工作都集中在静态旋涂上，没有考虑液滴撞击时的动能对辅助液膜铺展的影响。

团队通过实验观察、数值模拟、理论分析相结合的方法对酒精液滴旋涂过程中不同阶段的特征参数如：铺展半径、液膜厚度、接触线速度等进行了定量分析。选用酒精是因为其表面张力、粘度以及密度与绝大多数有机溶剂类似，因此对酒精液滴动态旋涂的结论具有较广泛的参考意义。团队还聚焦研究单个液滴的动态旋涂行为，因为简单滴落的酒精液滴大小为毛细尺度（直径为2.3毫米），重复性高，液体用量可以覆盖一块典型的光伏器件基片面积。

图1：动态旋涂实验示意图

研究者使用多台高速相机从不同角度（从45°斜视和侧视）对液膜铺展进行观察（图1）。视频展示（图2a），液滴铺展过程中存在两个区域：一是中间大部分的平滑薄膜区域，二是在边缘凸起的圆环边缘（称之为“毛细脊”或capillary ridge）。毛细脊的演化也是研究者关注的问题，因为毛细脊可以看做液体圆柱的一部分，容易受到Rayleigh-Plateau失稳的影响行成周期性的起伏，最终分裂形成指状失稳(fingering instability)。动态旋涂液滴下落对心准确显得极为重要，良好的对心可以有效延缓指状失稳的产生。为了测量动态旋涂过程中液膜的厚度，研究者设计了一种新颖的荧光成像测量方法。通过在酒精中掺混荧光染色剂（罗丹明6G），再用均匀的紫外光照射，根据Lambert定律和对已知膜厚的标定，可以由视频中的亮度得出每一帧图像的膜厚分布。这种方法可以从高速视频（图2b）中解析几微米的液膜和百微米级的毛细脊（图2c）。实验测量与数值模拟结果能够很好地吻合（图3）。

对于液滴对静态基底的冲击，韦伯数描述了惯性作用和毛细作用之间的相对重要性，并支配了液滴的变形和铺展行为。在动态旋涂过程中，韦伯数也起着重要作用，但主要在于惯性铺展阶段。在离心铺展阶段，由于离心加速度产生的特征压力为ρω2R2(R为液膜半径)，毛细压为~γ/h(h为液膜厚度)，因此可以将旋转邦德数Bor 定义为两个量的比值Bor = ρω2V/γ，其中V为液滴体积。同时，Bor也确定了指状不稳定性发生的临界半径Rc，为避免指状不稳定性从而导致液膜形貌缺陷，最终成膜的半径应小于Rc。

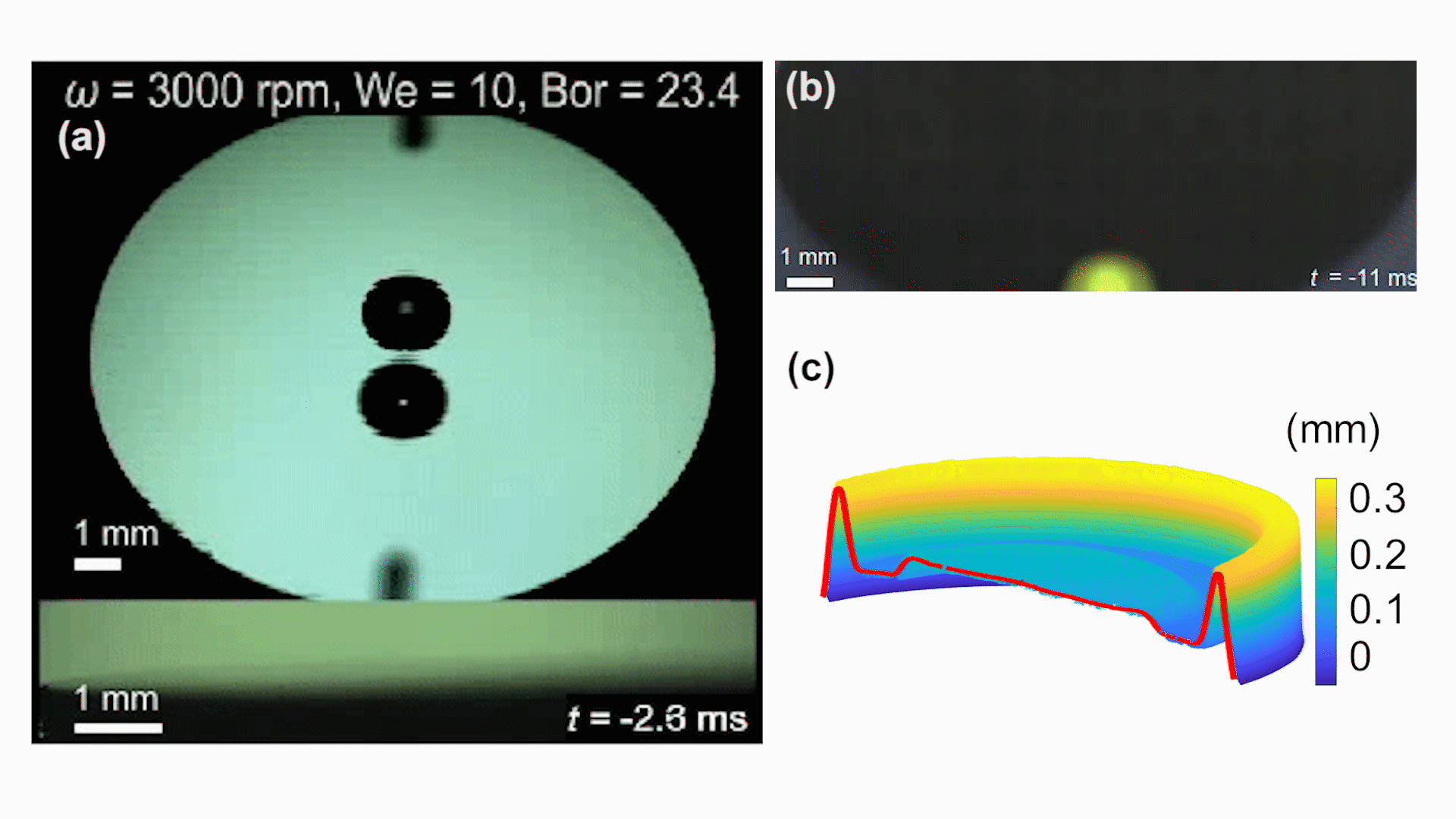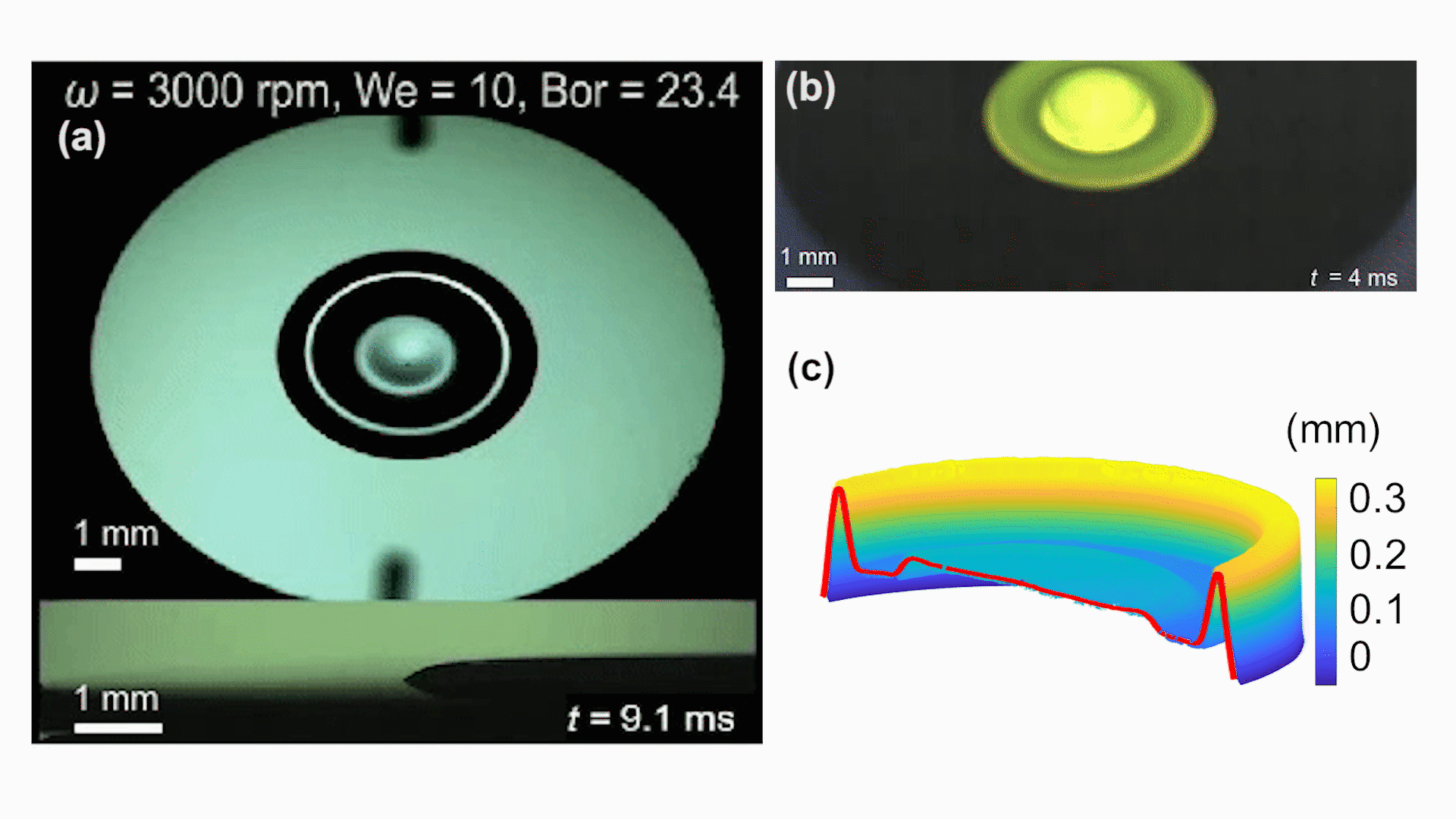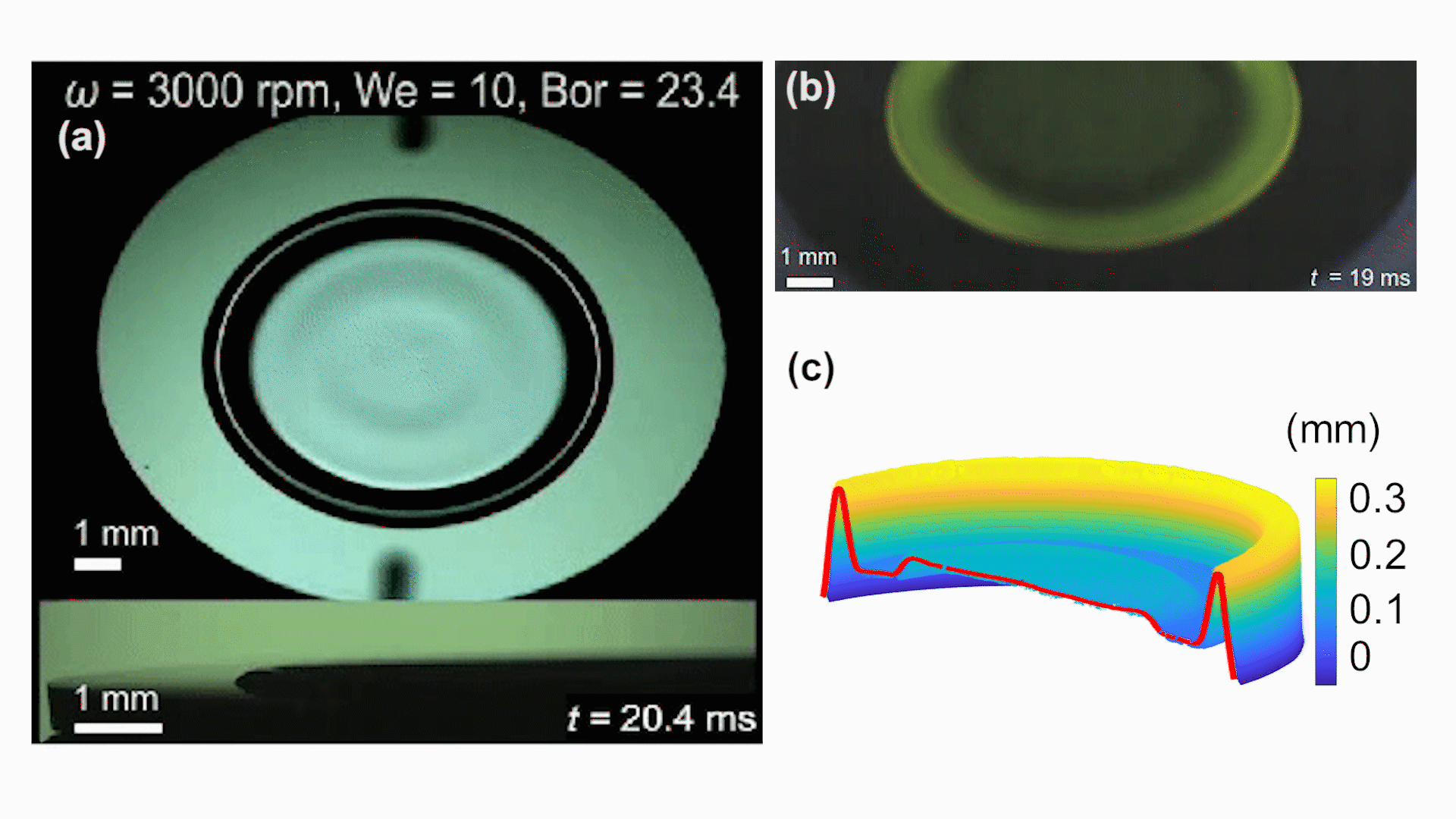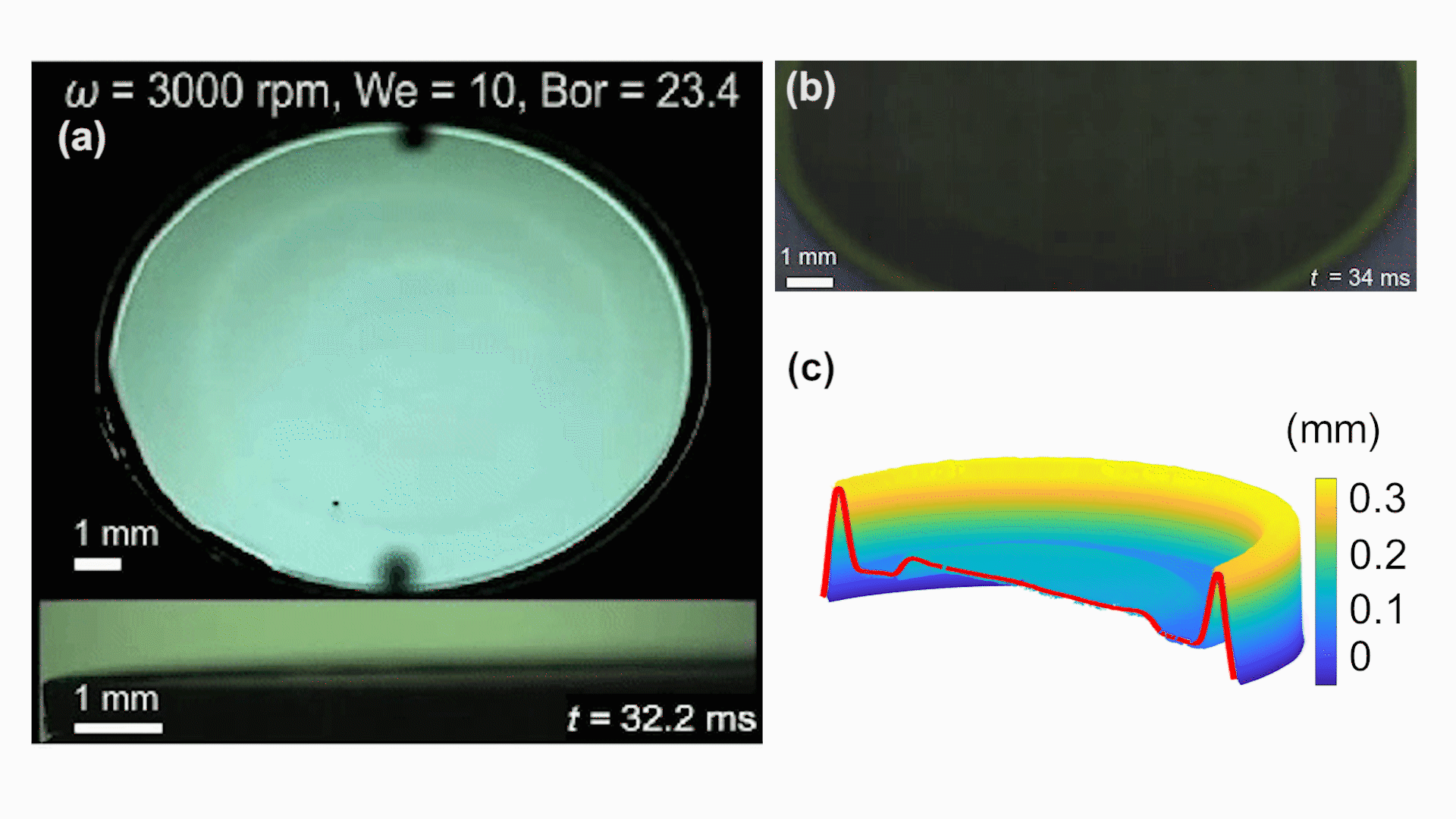
图2（a）45°斜视和侧视同步高速摄影测量铺展半径和毛细脊宽度；（b）基于罗丹明6G酒精溶液的荧光法测量液膜厚度;（c）荧光成像的图像处理后获得的液滴铺展轮廓

图3 实验模拟结果对比图

研究者系统地对不同We和Bor条件下的液膜的特征参数（铺展半径、膜厚、毛细脊特征、接触角）进行观测和分析。研究发现，动态旋涂过程中液滴铺展可分为惯性驱动和离心驱动的两个阶段，两者的分界点标志是液滴的最低铺展速度。在惯性驱动阶段，由液滴重力势能转化的动能与表面能在液滴总能量中占比较大，液滴铺展仍遵循液滴撞击静止基底的规律，即铺展半径随时间1/2幂指数增长；在离心驱动阶段，则是1.2次幂的关系，即液滴铺展在这一阶段在离心驱动下呈缓慢加速趋势。同时，膜厚与时间满足-1/2的幂指数规律，这一发现考虑了空气流动的影响，且与基于润滑理论（忽略表面张力）的结论一致。研究还发现，两个铺展阶段之间的过渡半径，即最低铺展速度时的铺展半径，与旋转邦德数无关（图3a），而与撞击时的韦伯数近似呈1/10次幂关系（图4b）。该结论为动态旋涂应用提供了重要理论指导。

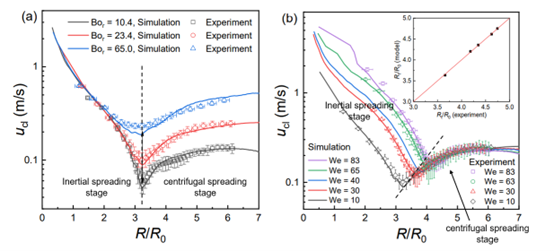
图4 铺展速度在不同条件下(a)相同韦伯数We=10，旋转邦德数Bor不同下的变化规律，和(b) 旋转邦德数Bor = 23.4，不同韦伯数下的变化规律

南科大2017级本科生潘昱铭为论文第一作者，邓巍巍和研究助理教授夏辉辉为共同通讯作者。南科大是论文第一单位。此项工作受到了国家自然科学基金和深圳市科创委的支持。

论文链接：https://www.cambridge.org/core/journals/journal-of-fluid-mechanics/article/abs/on-axisymmetric-dynamic-spin-coating-with-a-single-drop-of-ethanol/A24C1621307B34148A6A3EA8C034D412